Tag: zernike

zernike 输入各对应点 对应的差值 就可以计算出像差

泽尼克多项式是一个正交多项式，分为奇偶两类。

奇多项式：

偶多项式：

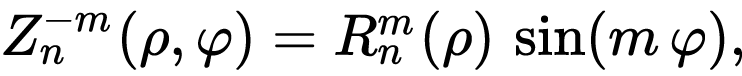
其中：

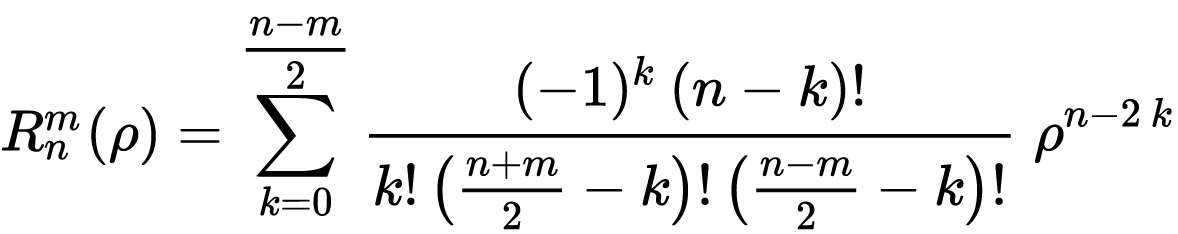
这里fai为方位角，范围[0-2pi]；p为径向距离，范围[0,1]；n-m大于等于0；

如果n-m=0，则R=0。

根据不同的m和n值，可以得到不同的多项式，用j表示不同的多项式，通常称为Noll序列：

n,m	0,0	1,1	1,−1	2,0	2,−2
j	1	2	3	4	5
n,m	2,2	3,−1	3,1	3,−3	3,3
j	6	7	8	9	10
n,m	4,0	4,2	4,−2	4,4	4,−4
j	11	12	13	14	15
n,m	5,1	5,−1	5,3	5,−3	5,5
j	16	17	18	19	20

jtonmtable 对应的就是这个序列

n m

1 0 0
2 1 1
3 1 -1
4 2 0
5 2 -2
6 2 2
7 3 -1
8 3 1
9 3 -3
10 3 3
11 4 0
12 4 2
13 4 -2
14 4 4
15 4 -4

azimtable 对应的就是 cos sin 角度的系数

cos sin

1 0 0
2 1 0
3 0 1
4 0 0
5 0 2
6 2 0
7 0 1
8 1 0
9 0 3
10 3 0
11 0 0
12 2 0
13 0 2
14 4 0
15 0 4

radialtable 对应的包括 根号系数了

Noll序列前15项泽尼克多项式为：

1	1
2	2ρcosθ
3	2ρsinθ
4	√3(2ρ2−1)
5	√6ρ2sin2θ
6	√6ρ2cos2θ
7	√3(3ρ3−2ρ)sinθ
8	√3(3ρ3−2ρ)cosθ
9	√8ρ3sin3θ
10	√8ρ3cos3θ
11	√5(6ρ4−6ρ2+1)
12	√10(4ρ4−3ρ2)cos2θ
13	√10(4ρ4−3ρ2)sin2θ
14	√10ρ4cos4θ
15	√10ρ4sin4θ